tldr; use einops.einsum

Machine learning is built of matrix algebra. Einstein summation notation (or einsum for short) makes matrix operations more intuitive and readable.

As you may know, the matrix multiplication that you learned in high school…

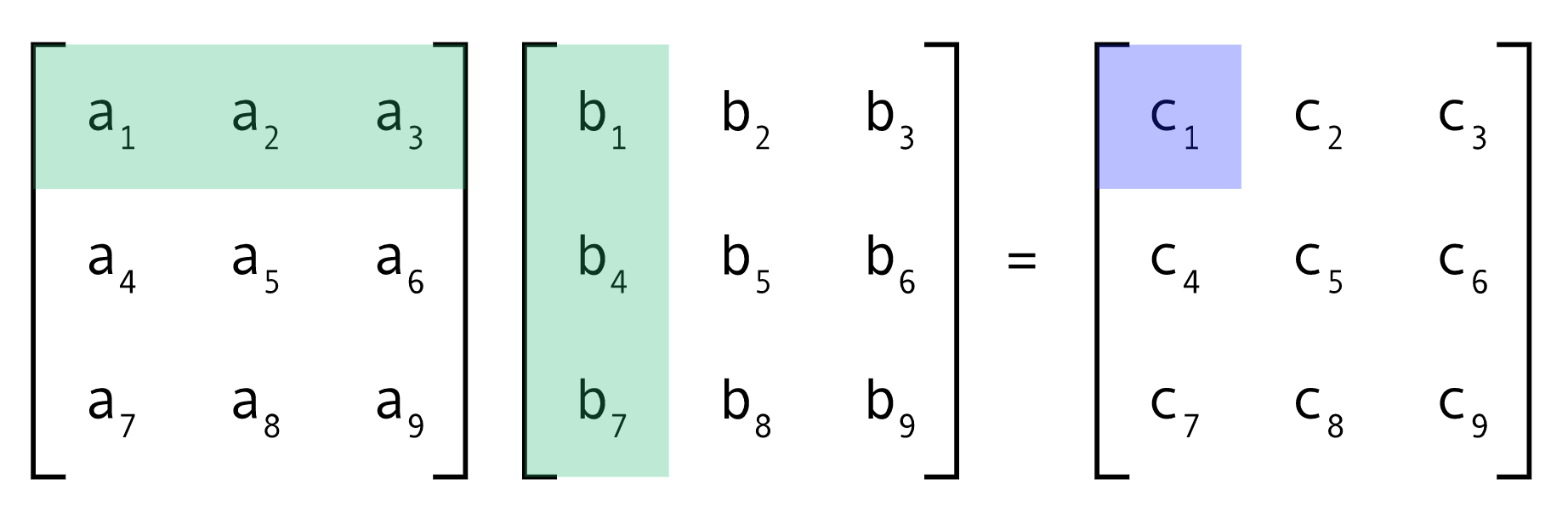
3x3 matrix multiplication
Calculating the 0,0th element of a matrix multiplication

Can be written algebraically as:

\[A_{ik} = \sum_j B_{ij} C_{jk}\]

In other words in order to get the (1,2) element of A we calculate:

\[A_{1,2} = \sum_j B_{1j} C_{j2}\]

i.e. take the dot product of the 1st row of B with the 2nd column of C.



In Einsum notation, to avoid having so many sigmas (\(\sum\)) flying around we adopt the convention that any indices that appear more than once are being summed over. Hence:

\[A_{ik} = \sum_j B_{ij} C_{jk}\]

can be written more simply as…

\[A_{ik} = B_{ij} C_{jk}\]



Both torch and numpy have einsum packages to allow you to use einsum notation for matrix operations. For example, we can write the above matrix multiplication in torch as:

import torch as t

A = t.einsum("ij,jk->ik", B, C)

The convention is that if a dimension only appears on the left side of the einsum then it’s summed over. So in the above we’re summing over the j dimension and keeping the i and k dimensions. That’s our classic matrix multiplication written in torch einsum notation1.

Great!

One issue when using torch.einsum though is that it’s not necessarily super clear what each letter means:

  • Was i a horizontal index (as in x,y coordinates) or is it a vertical index (as in tensor indexing?)
  • Was e embedding dimension or expert number?
  • Was h height, head dimension or hidden dimension?

To get around this ambiguity, it’s common to see PyTorch code where in the docstring each of the letters is defined. This isn’t a very natural pattern - it’s like if all of your variable names in code had to be single letters and you had another file which would act as a dictionary for what each letter actually meant! shudders.

One of the most useful lines of the Zen of Python is Explicit is better than Implicit. Following this principle, we would like to be able to write the variable names in the einsum string itself. Without this, it’s harder to read and means you’re always looking back when trying to understand or debug the code.

Enter einops

Einops is a tensor manipulation package that can be used with PyTorch, NumPy, Tensorflow and Jax. It offers a nice API but we’ll focus on einsums which we can now use with full variable names rather than single letters! It makes your ML code so much clearer instantly.

For example let’s write the multi-query attention operation.


Multi Query Attention
Multi-Query Attention is a type of attention where we have multiple query heads (like in Multi-Head Attention) but only a single key and value head per layer


import torch as t
from einops import einsum

def multi_query_attention(Q: t.Tensor, K: t.Tensor, V: t.Tensor) -> t.Tensor
    _, _, head_dim = K.shape
    attn_scores = einsum(Q, K,
        "batch head seq1 head_dim, batch seq2 head_dim -> batch head seq1 seq2")
    attn_matrix = t.softmax(attn_scores / head_dim ** 0.5)
    out =  einsum(attn_matrix, V,
        "batch head seq1 seq2, batch seq2 head_dim -> batch head seq1 head_dim")
    return out

One catch here is that we want to have the sequence length represented twice for \(QK^T\) but we don’t want to sum over it. To solve this we give them two different names like seq1 and seq2

The nice things about this are that we didn’t need to write a glossary for what random variables b or h were supposed to mean, we can just read it off.

Also note that typically when computing attention, we need to calculate \(QK^T\). Here we didn’t need to worry about how exactly to take the transpose - we just give the dimension names and the correct transposes are done for the multiplication to make sense!

Einops also offers great functions for rearranging, reducing and repeating tensors which are also very useful.

The World If Everyone Used Einops

That’s all! Just trying to make those inscrutable matrix multiplications, a little more scrutable. 



  1. I feel like a fancy chef here. For our appetiser we have Matrix Multiplication Done Four Ways and so on… ↩